Let us see how the ideal gas law is consistent with the behavior of filling the tire when it is pumped slowly and the temperature is constant. At first, the pressure [/latex] is essentially equal to atmospheric pressure, and the volume [/latex] increases in direct proportion to the number of atoms and molecules [/latex] put into the tire. Once the volume of the tire is constant, the equation [/latex] predicts that the pressure should increase in proportion to the number N of atoms and molecules. The behavior of gases can be described by several laws based on experimental observations of their properties.
The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons's law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles's law). The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle's law).
Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro's law). Avogadro's Number, the ideal gas constant, and both Boyle's and Charles' laws combine to describe a theoretical ideal gas in which all particle collisions are absolutely equal. The laws come very close to describing the behavior of most gases, but there are very tiny mathematical deviations due to differences in actual particle size and tiny intermolecular forces in real gases. Nevertheless, these important laws are often combined into one equation known as the ideal gas law. Using this law, you can find the value of any of the other variables — pressure, volume, number or temperature — if you know the value of the other three. In the ideal gas model, the volume occupied by its atoms and molecules is a negligible fraction of VV size 12 .
The ideal gas law describes the behavior of real gases under most conditions. Note, for example, that NN size 12 is the total number of atoms and molecules, independent of the type of gas. Gases whose properties of P, V, and T are accurately described by the ideal gas law are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter. Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures.
Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships , then put them together in the ideal gas law. When air is pumped into a deflated tire, its volume first increases without much increase in pressure.
When the tire is filled to a certain point, the tire walls resist further expansion and the pressure increases with more air. Once the tire is inflated, its pressure increases with temperature.At room temperatures, collisions between atoms and molecules can be ignored. In this case, the gas is called an ideal gas, in which case the relationship between the pressure, volume, and temperature is given by the equation of state called the ideal gas law. Hydrogen gas has the chemical formula H2 and the molecular weight of 2. This gas is the lightest substance among all chemical compounds and the most abundant element in the universe. Hydrogen gas has also drawn significant attention as a potential energy source.
Hydrogen can be obtained, for example, by electrolysis of the water. You calculate the amount of hydrogen in moles either from the gas mass or using the ideal gas law. The ideal gas law is written for ideal or perfect gases.
You can use values for real gases so long as they act like ideal gases. To use the formula for a real gas, it must be at low pressure and low temperature. Increasing pressure or temperature raises the kinetic energy of the gas and forces the molecules to interact. While the ideal gas law can still offer an approximation under these conditions, it becomes less accurate when molecules are close together and excited. Usually the particles counted are chemically identical entities, individually distinct. For example, a solution may contain a certain number of dissolved molecules that are more or less independent of each other.
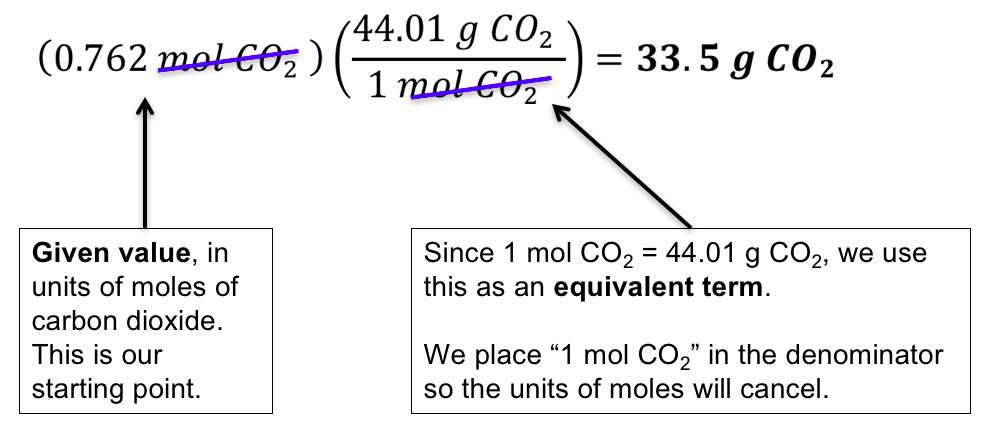
However, in a solid the constituent particles are fixed and bound in a lattice arrangement, yet they may be separable without losing their chemical identity. Thus the solid is composed of a certain number of moles of such particles. Thus, common chemical conventions apply to the definition of the constituent particles of a substance, in other cases exact definitions may be specified. The mass of 1 mole of a substance is equal to its relative atomic or molecular mass in grams. The moles to liters/liters to moles conversion is straightforward and is based on the fact that the ideal gas equation is a good approximation for many common gases at standard temperature and pressure. Thus, we can rearrange terms in the ideal gas equation and write them like this .
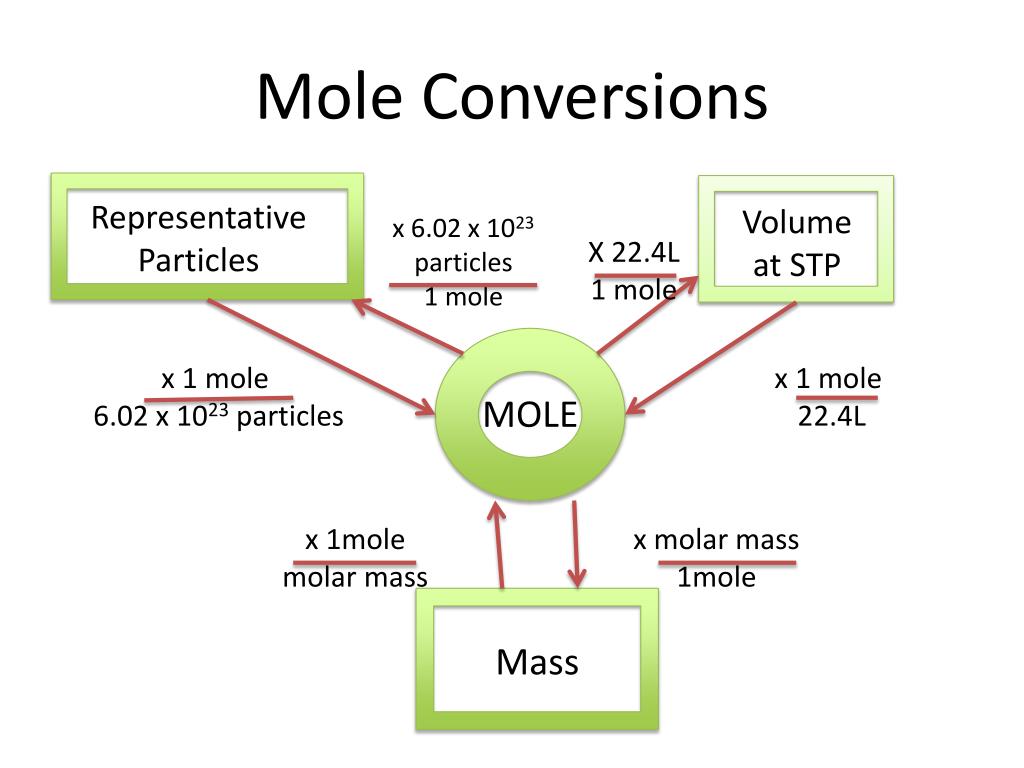
To get to moles, use the equation and the molar ratios shown. To get to volume, use the molar volume of gas constants. To get to mass, use the atomic/molecular masses shown in the periodic table. The ideal gas law allows us to calculate the value of the fourth variable for a gaseous sample if we know the values of any three of the four variables .
Some applications are illustrated in the following examples. The approach used throughout is always to start with the same equation—the ideal gas law—and then determine which quantities are given and which need to be calculated. Let's begin with simple cases in which we are given three of the four parameters needed for a complete physical description of a gaseous sample. Thus the ideal gas law does a good job of approximating the behavior of real gases at STP. The ideal gas law can be considered to be another manifestation of the law of conservation of energy (see Chapter 7.6 Conservation of Energy).
Work done on a gas results in an increase in its energy, increasing pressure and/or temperature, or decreasing volume. This increased energy can also be viewed as increased internal kinetic energy, given the gas's atoms and molecules. The ideal gas law can be considered to be another manifestation of the law of conservation of energy . At room temperatures, collisions between atoms and molecules can be ignored.
In grade 10 learners learnt about the molar volume of gases. This concept is refreshed here and then expanded on to cover any number of moles of gases. The ideal gas law formula states that pressure multiplied by volume is equal to moles times the universal gas constant times temperature. In chemistry, it has been known since Proust's law of definite proportions that knowledge of the mass of each of the components in a chemical system is not sufficient to define the system.
Amount of substance can be described as mass divided by Proust's "definite proportions", and contains information that is missing from the measurement of mass alone. As demonstrated by Dalton's law of partial pressures , a measurement of mass is not even necessary to measure the amount of substance . There are many physical relationships between amount of substance and other physical quantities, the most notable one being the ideal gas law . The term "mole" was first used in a textbook describing these colligative properties. The molar volume of gas at STP, standard temperature and pressure (0°C or 273K, 100 kPa pressure) is 22.4 litres per mole (22.4 L/mol).
In other words, one mole of atoms of a pure ideal gas at 0°C will fill 22.4 litres of space. The molar volume of gas at room temperature (25°C, 298K) and pressure is 24 litres per mole (24 L/mol). Chemistry is the study of matter, from individual atoms and ions to large biomolecules.
With Wolfram|Alpha, you can explore data about chemical compounds, the reactions they undergo, solubility and chemical graph theory. It also has information about chemical quantities, unit conversion, molarity calculations and stoichiometry. Use Wolfram|Alpha to answer your chemistry questions, whether they are for homework or general curiosity. The reaction of a copper penny with nitric acid results in the formation of a red-brown gaseous compound containing nitrogen and oxygen.
A sample of the gas at a pressure of 727 mmHg and a temperature of 18°C weighs 0.289 g in a flask with a volume of 157.0 mL. Calculate the molar mass of the gas and suggest a reasonable chemical formula for the compound. A common use of Equation 10.23 is to determine the molar mass of an unknown gas by measuring its density at a known temperature and pressure. This method is particularly useful in identifying a gas that has been produced in a reaction, and it is not difficult to carry out. A flask or glass bulb of known volume is carefully dried, evacuated, sealed, and weighed empty.
It is then filled with a sample of a gas at a known temperature and pressure and reweighed. The difference in mass between the two readings is the mass of the gas. The volume of the flask is usually determined by weighing the flask when empty and when filled with a liquid of known density such as water.
The use of density measurements to calculate molar masses is illustrated in Example 10. One mole always contains [/latex] particles , independent of the element or substance. A mole of any substance has a mass in grams equal to its molecular mass, which can be calculated from the atomic masses given in the periodic table of elements.
The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm. If the temperature is in kelvin, volume and temperature are directly proportional. Charles's law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant. Atoms and molecules are close together in solids and liquids.
Thus, gases have lower densities than liquids and solids. Density is mass per unit volume, and volume is related to the size of a body, such as a sphere, cubed. So if the distance between atoms and molecules increases by a factor of 10, then the volume occupied increases by a factor of 1,000, and the density decreases by a factor of 1,000. If themolecular massof a gas is known, the ideal gas law can be manipulated to find the density of the gas. It's just a matter of plugging in the right variables and performing a few calculations.
It is important to check your answer to be sure that it makes sense, just in case you have accidentally inverted a quantity or multiplied rather than divided. Because we know that gas volume decreases with decreasing temperature, the final volume must be less than the initial volume, so the answer makes sense. We could have calculated the new volume by plugging all the given numbers into the ideal gas law, but it is generally much easier and faster to focus on only the quantities that change.
B Make sure that all quantities are given in units that are compatible with the units of the gas constant. If necessary, convert them to the appropriate units, insert them into the equation you have derived, and then calculate the number of moles of hydrogen gas needed. You can adapt to the set of units you'd like to use just by changing the gas constant. Here are the constants and the units of pressure, temperature and volume that go with them. While, when using gas laws like Charles' law and the Gay-Lussac law, it's OK to use Celsius temperatures , it's important to use Kelvin temperatures in the ideal gas law. Can be interpreted to mean that for each 2 mol dihydrogen and 1 mol dioxygen that react, 2 mol of water form.
The mole may also be used to measure the amount of atoms, ions, electrons, or other entities. This means equal amounts of moles of gases occupy the same volume under the same conditions of temperature and pressure. Thus gases have lower densities than liquids and solids. Density is mass per unit volume, and volume is related to the size of a body cubed. So if the distance between atoms and molecules increases by a factor of 10, then the volume occupied increases by a factor of 1000, and the density decreases by a factor of 1000. One mole always contains 6.02 × 1023 particles , independent of the element or substance.
Use the ideal gas law to calculate pressure change, temperature change, volume change, or the number of molecules or moles in a given volume. B Convert all known quantities to the appropriate units for the gas constant being used. Substitute the known values into your equation and solve for the molar mass.
How To Find The Number Of Moles Of A Gas Is defined as a hypothetical gaseous substance whose behavior is independent of attractive and repulsive forces and can be completely described by the ideal gas law. In reality, there is no such thing as an ideal gas, but an ideal gas is a useful conceptual model that allows us to understand how gases respond to changing conditions. As we shall see, under many conditions, most real gases exhibit behavior that closely approximates that of an ideal gas. The ideal gas law can therefore be used to predict the behavior of real gases under most conditions. This special section on the ideal gas law follows from the section on gas laws. You might want to begin there for a better understanding of where the ideal gas law originates.
You might also benefit from reading about the kinetic molecular theory of gases. The most common molar volume is the molar volume of an ideal gas at standard temperature and pressure (273 K and 1.00 atm). Read on to find out more about the ideal gas law, moles, and examples & tips on how to resolve chemical equations. The answer lies in the large separation of atoms and molecules in gases, compared to their sizes, as illustrated in Figure 2. Because atoms and molecules have large separations, forces between them can be ignored, except when they collide with each other during collisions.
The motion of atoms and molecules is fast, such that the gas occupies all of the accessible volume and the expansion of gases is rapid. In contrast, in liquids and solids, atoms and molecules are closer together and are quite sensitive to the forces between them. The kinetic energy per unit of temperature of one mole of a gas is a constant value, sometimes referred to as the Regnault constant, named after the French chemist Henri Victor Regnault. Regnault studied the thermal properties of matter and discovered that Boyle's law was not perfect. When the temperature of a substance nears its boiling point, the expansion of the gas particles is not exactly uniform. Decreasing the volume of the container forces the particles to collide more often, so the pressure is increased.
A good example of this is when you fill a tire with air. As more air goes in, the gas molecules get packed together, reducing their volume. As long as the temperature stays the same, the pressure increases. It is possible to calculate the volume of one mole of gas at standard temperature and pressure using what we now know about gases.
At the end of the chapter learners bring together all the concepts that they have learnt into this topic. Learners are introduced to the idea that the balanced chemical equation can be used to calculate any quantity of a substance from any of the other products or reactions in that reaction. Step 2 Make a list of what quantities are given, or can be inferred from the problem as stated—identify the known quantities. Convert known values into proper SI units—K for temperature, Pa for pressure, m3m3 size 12 for volume, molecules for NN size 12 , and moles for nn size 12 .






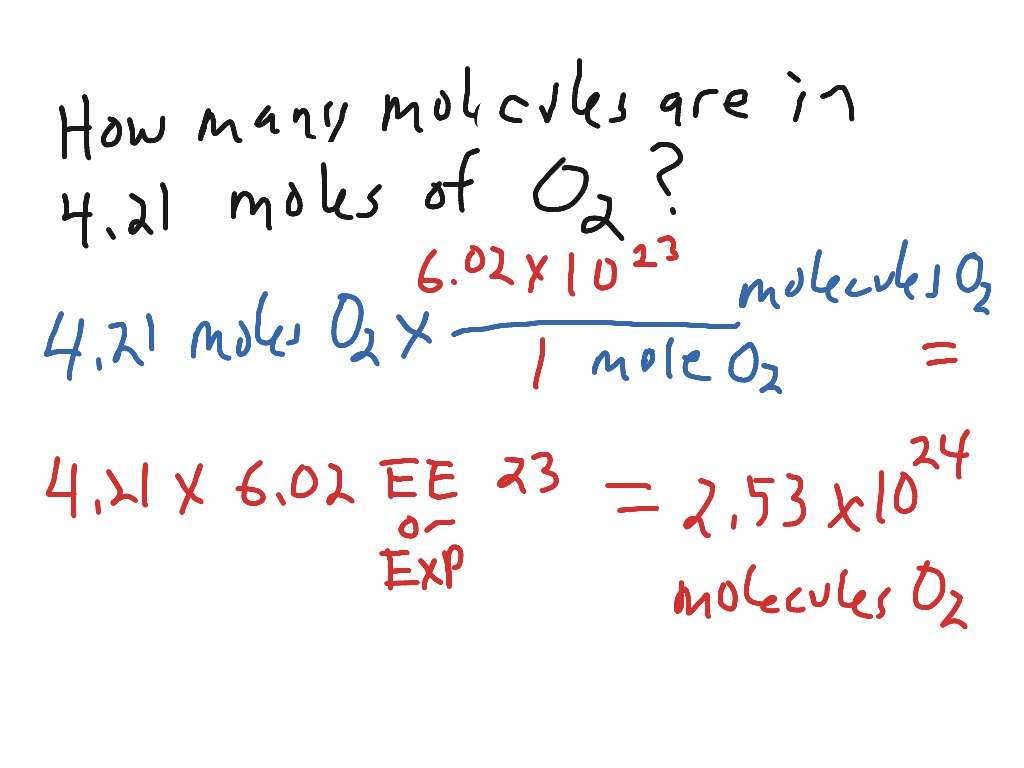


















No comments:
Post a Comment
Note: Only a member of this blog may post a comment.